在Java中创建魔方
在Java中创建魔方
在这篇文章中,我们将探讨如何创建魔方。我们将了解什么是魔方,创建它们的算法是什么,以及如何在Java中实现它们。
2. 什么是魔方?
魔方是一种数学谜题。我们从一个大小为 n×n 的正方形开始,需要用数字填充,使得每个数字在1到 n² 之间恰好出现一次,并且每一行、每一列和对角线的和都相同。
例如,一个3×3的魔方可能是这样的:
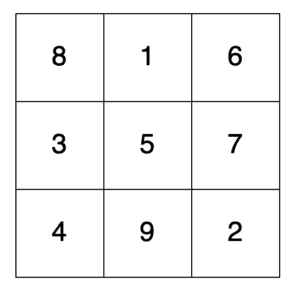
在这里我们可以看到每个单元格都有不同的数字,介于1和9之间。我们还可以看到每一行、每一列和对角线的和都是15。
实际上,这里有一个额外的检查。每一行、每一列和对角线的和也等于一个可以通过仅知道 n 来计算的值。具体来说:
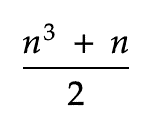
所以,对于我们的3×3正方形,这个值是 (3³ + 3)/2 = 15。
事实上,有三种相对简单的算法可以用来生成这些魔方,这取决于正方形的大小:
- 奇数边长
- 双倍:边长为偶数。这是当每边是4的倍数时。
- 单倍:边长为偶数。这是当每边是2的倍数但不是4的倍数时。
我们将逐一查看这些算法以及如何在Java中生成它们。
3. 验证魔方
在我们能够生成我们的魔方之前,我们首先需要能够证明给定的正方形确实符合要求。也就是说,每一行、每一列和对角线的和都是相同的值。
在我们开始之前,让我们定义一个类来表示我们的正方形:
public class MagicSquare {
private int[][] cells;
public MagicSquare(int n) {
this.cells = new int[n][];
for (int i = 0; i `< n; ++i) {
this.cells[i] = new int[n];
}
}
public int getN() {
return cells.length;
}
public int getCell(int x, int y) {
return cells[x][y];
}
public void setCell(int x, int y, int value) {
cells[x][y] = value;
}
}
这只是一个围绕二维整数数组的包装器。然后我们确保数组的大小正确,并且我们可以轻松地访问数组中的单个单元格。
现在我们有了这个,让我们写一个方法来验证正方形确实是一个魔方。
首先,我们将计算我们期望的行、列和对角线的和值:
int n = getN();
int expectedValue = ((n * n * n) + n) / 2;
接下来,我们将开始求和并检查它们是否符合预期。我们先从对角线开始:
// 对角线
if (IntStream.range(0, n).map(i ->` getCell(i, i)).sum() != expectedValue) {
throw new IllegalStateException("主对角线不是预期的值");
}
if (IntStream.range(0, n).map(i -> getCell(i, n - i - 1)).sum() != expectedValue) {
throw new IllegalStateException("副对角线不是预期的值");
}
这只是从0到 n 迭代,抓住每个点上的对角线上的每个单元格并求和。
接下来,行和列:
// 行
IntStream.range(0, n).forEach(y -> {
if (IntStream.range(0, n).map(x -> getCell(x, y)).sum() != expectedValue) {
throw new IllegalStateException("行不是预期的值");
}
});
// 列
IntStream.range(0, n).forEach(x -> {
if (IntStream.range(0, n).map(y -> getCell(x, y)).sum() != expectedValue) {
throw new IllegalStateException("列不是预期的值");
}
});
在这里,我们适当地迭代每一行或列的所有单元格,并求和所有这些值。如果在这些情况下任何一个的值与我们预期的不同,我们将抛出一个异常,表明出了问题。
4. 生成魔方
现在我们可以正确验证任何给定的正方形是否是魔方。所以我们现在需要能够生成它们。
我们之前看到,根据正方形的大小,这里可以使用三种不同的算法。我们将依次查看每一种。
4.1. 奇数大小正方形的算法
我们将首先看到的算法是用于每边有奇数个单元格的正方形。
当生成这种大小的魔方时,我们总是首先将第一个数字放在第一行中间的单元格中。然后我们按照以下方式放置每一个后续的数字:
- 首先,我们尝试将其放在上一个单元格的正上方和右侧的单元格中。在这样做时,我们在边缘处进行包装,例如,在第一行之后,我们会移动到底部行。
- 如果这个期望的单元格已经被占据,我们则将下一个数字放在上一个单元格的正下方。同样,在这样做时,我们在边缘处进行包装。
例如,在我们的3×3正方形中,我们从第一行中间的单元格开始。然后我们向上和向右移动,包装到找到右下角的单元格:
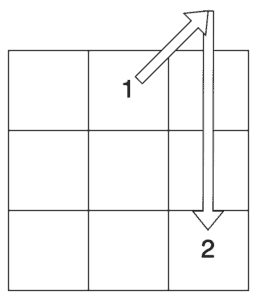
从这里,我们向上和向右移动以填充中间左侧的单元格。在这之后,向上和向右移动会回到第一个单元格,所以我们必须向下移动到左下角的单元格:
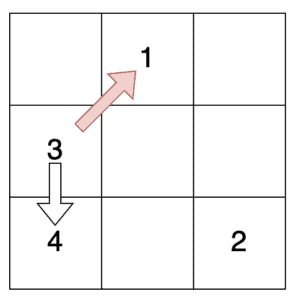
如果我们继续这样做,我们最终会用有效的魔方填充每一个正方形。
4.2. 奇数大小正方形的实现
那么我们在Java中如何实现这一点呢?
首先,让我们放置我们的第一个数字。这在第一行的中心单元格中:
int y = 0;
int x = (n - 1) / 2;
setCell(x, y, 1);
完成这个之后,我们将循环遍历所有其他的数字,依次放置每一个:
for (int number = 2; number `<= n * n; ++number) {
int nextX = ...;
int nextY = ...;
setCell(nextX, nextY, number);
x = nextX;
y = nextY;
}
现在我们只需要确定要使用什么值作为 nextX 和 nextY。
首先,我们将尝试向上和向右移动,必要时进行包装:
int nextX = x + 1;
if (nextX == n) {
nextX = 0;
}
int nextY = y - 1;
if (nextY == -1) {
nextY = n - 1;
}
然而,我们还需要处理下一个单元格已经被占据的情况:
if (getCell(nextX, nextY) != 0) {
nextX = x;
nextY = y + 1;
if (nextY == n) {
nextY = 0;
}
}
将所有这些放在一起,我们就实现了生成任何奇数大小魔方的实现。 例如,使用此方法生成的9×9正方形如下所示:
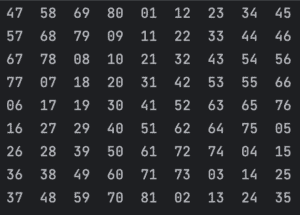
4.3. 双倍偶数大小正方形的算法
上述算法适用于奇数大小的正方形,但不适用于偶数大小的正方形。 实际上,对于这些,我们需要根据确切的大小使用两种算法之一。
双倍偶数正方形是指边长是4的倍数的正方形——例如4×4、8×8、12×12等。 为了生成这些,我们需要在我们的正方形中分离出4个特殊区域。这些区域是每个边缘 n/4 的单元格,同时距离角落超过 n/4:
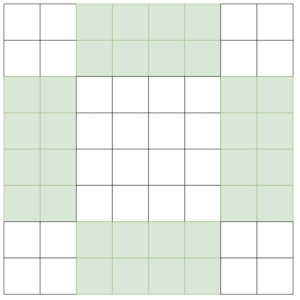
完成这个之后,我们现在填充数字。这是通过两次传递完成的。第一次传递从左到右开始,每次我们在未突出显示的单元格上时,我们都会添加序列中的下一个数字:
第二次传递与第一次完全相同,但是从右下角开始,向右向左运行,并且只向突出显示的单元格加数字:
此时,我们已经得到了有效的魔方。
4.4. 双倍偶数大小正方形的实现
为了在Java中实现这一点,我们需要使用两种技术。
首先,我们实际上可以在一次传递中添加所有的数字。如果我们在未突出显示的单元格上,那么我们就如前所述,但如果我们在突出显示的单元格上,那么我们就会从 n² 开始倒数:
int number = 1;
for (int y = 0; y < n; ++y) {
for (int x = 0; x < n; ++x) {
boolean highlighted = ...;
if (highlighted) {
setCell(x, y, (n * n) - number + 1);
} else {
setCell(x, y, number);
}
number += 1;
}
}
现在我们只需要弄清楚我们认为哪些是突出显示的正方形。我们可以通过检查我们的 x 和 y 坐标是否在范围内来做到这一点:
if ((y < n/4 || y >`= 3*n/4) && (x >= n/4 && x `< 3*n/4)) {
highlighted = true;
} else if ((x < n/4 || x >`= 3*n/4) && (y >= n/4 && y < 3*n/4)) {
highlighted = true;
}
我们的第一条件是正方形顶部和底部的突出显示区域,而我们的第二个条件是正方形左侧和右侧的突出显示区域。我们可以看到它们实际上是相同的,只是在检查中交换了 x 和 y。在这两种情况下,都是我们在该侧的正方形的 1/4 之内,并且在相邻角落之间 1/4 和 3/4 的距离之内。
将所有这些放在一起,我们就实现了生成任何双倍偶数大小魔方的实现。 例如,我们使用此方法生成的8×8正方形如下所示:
4.5. 单倍偶数大小正方形的算法
我们最后的正方形大小是倍偶数正方形。也就是说,边长可以被2整除但不能被4整除。这也要求边长至少是6个单元格长——没有2×2魔方的解决方案,所以6×6是我们可以解决的最小的单倍偶数魔方。
我们首先将它们分成四分之一——每个都是奇数大小的正方形。然后使用与奇数大小魔方相同的算法进行填充,只是为每个象限分配不同的数字范围——从左上象限开始,然后是右下、左上和最后左下:
一旦我们使用我们的奇数大小算法填充了所有的正方形,我们仍然没有得到一个有效的魔方。 此时我们会注意到所有的列加起来都是正确的数字,但行和对角线不是。然而,我们也会注意到上半部分的所有行加起来都是同一个数字,下半部分的行也是如此:
我们可以通过在上下两半之间执行一些交换来解决这个问题,如下所示:
- 我们左上象限的顶行中,中心左侧的每个单元格。
- 我们左上象限的底行中,中心左侧的每个单元格。
- 这两行之间的每一行中的相同数量的单元格,但开始时向右一个单元格。
- 右上象限的每一行中比这些少一个单元格,但从右侧开始。
然后看起来像这样:
现在这是一个有效的魔方,每一行、每一列和对角线都加起来得到相同的值——在这种情况下是505。
4.6. 单倍偶数大小正方形的实现
这个的实现将建立在我们为奇数大小正方形所做的事情上。 首先我们需要计算一些用于生成的值:
int halfN = n/2;
int swapSize = n/4;
注意我们是如何将 swapSize 计算为 n/4 并将其存储到一个int中的。这有效地进行了向下取整,所以对于 n=10,我们将得到一个 swapSize 值为2。
接下来,我们需要填充我们的网格。我们将假设我们已经有一个函数来执行奇数大小的正方形算法,只是适当地偏移:
populateOddArea(0, 0, halfN, 0);
populateOddArea(halfN, halfN, halfN, halfN * halfN);
populateOddArea(halfN, 0, halfN, (halfN * halfN) * 2);
populateOddArea(0, halfN, halfN, (halfN * halfN) * 3);
现在我们只需要执行我们的交换。同样,我们将假设我们有一个函数来交换我们正方形中的单元格。
在左象限中交换单元格是通过从左侧开始迭代 swapSize 并执行交换来完成的:
for (int x = 0; x < swapSize; ++x) {
swapCells(x, 0, x, halfN); // 顶行
swapCells(x, halfN - 1, x, n - 1); // 底行
// 所有中间行。
for (int y = 1; y < halfN - 1; ++y) {
swapCells(x + 1, y, x + 1, y + halfN);
}
}
最后,我们交换右象限中的单元格。这是通过从右侧开始迭代 swapSize – 1 并执行交换来完成的:
for (int x = 0; x < swapSize - 1; ++x) {
for (int y = 0; y < halfN; ++y) {
swapCells(n - x - 1, y, n - x - 1, y + halfN);
}
}
将所有这些放在一起,我们就实现了生成任何单倍偶数大小魔方的实现。 例如,我们使用此方法生成的10×10正方形如下所示:
5. 总结
在这里,我们研究了用于创建魔方的算法,并看到了我们如何在Java中实现它们。
和往常一样,我们可以在GitHub上找到本文的所有代码。 OK