Roaring Bitmap 简介
Roaring Bitmap 简介
在本教程中,我们将学习关于 roaring bitmap 的知识。我们将使用一些基本的集合操作作为 roaring bitmap 的示例,并在 Java 中执行 RoaringBitmap 和 BitSet 之间的性能测试。
roaring bitmap 数据结构通常用于分析、搜索和大数据项目,因为它具有高性能和压缩比。它的灵感来自于位图索引,这是一种有效表示数字数组的数据结构。它类似于 Java 的 BitSet,但是经过压缩。
在压缩大整数集合的同时保持对各个元素的快速访问是 roaring bitmap 的重要优势。Roaring bitmap 内部使用不同类型的容器来实现这一点。
Roaring Bitmap 的工作原理
roaring bitmap 是由不相交子集组成的无符号整数集合。每个子集都有一个 16 位的键索引,并且可以容纳大小为 2^16 的范围中的值。这允许将无符号 32 位整数存储为 Java 的 short 类型,因为在最坏的情况下,只需要 16 位来表示一个 32 位的值。容器大小的选择还确保了,在最坏的情况下,容器仍然适合现代 CPU 的 L1 缓存。
以下图像表示 roaring bitmap 结构的外观:

我们的整数的 16 位最高有效位是桶或块键。每个数据块表示值范围区间 (0 `<= n < 2^16) 的基础。此外,如果没有数据在值范围内,就不会创建块。
下一个图像是一个包含不同数据的 roaring bitmap 的示例:
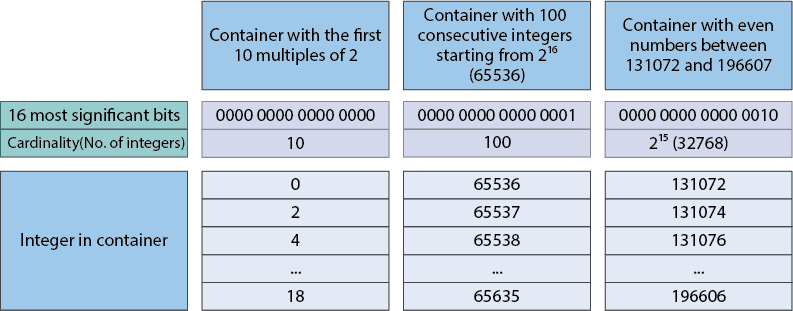
在第一个块中,我们存储了前 10 个 2 的倍数。此外,在第二个块中,我们有从 65536 开始的 100 个连续整数。图像中的最后一个块在 131072 和 19660 之间有偶数。
Roaring Bitmap 内部的容器
在 roaring bitmap 中有三种主要类型的容器 - Array、Bitmap 和 Run 容器。根据分区集的特性,Run 容器、Bitmap 容器或 Array 容器是用于持有分区数据的容器的实现。
当我们向 roaring bitmap 添加数据时,它内部会根据值是否适合容器键覆盖的范围来决定是创建一个新容器还是更改现有容器。
4.1. Roaring Bitmap 的 Array 容器
Array 容器不压缩数据,并且只持有少量数据。它所占用的空间与它所持有的数据量成正比:每个都是两个字节。
Array 容器使用的数据类型是 short 数据类型。整数按排序顺序存储。
此外,数组的初始容量是四个,并且元素的最大数量是 4096。数组容量是动态变化的。然而,当元素数量超过 4096 时,roaring bitmap 内部会将 Array 容器转换为 Bitmap 容器。
让我们来看一个在 roaring bitmap 中插入数据到 Array 容器的示例。我们有数字 131090。16 位最高有效位是 0000 0000 0000 0010,这是我们的键。低位的 16 位是 0000 0000 0001 0010。当我们将其转换为十进制基数时,它的值是 18。现在,插入数据后,这是我们的 roaring bitmap 结构:

我们可以注意到,在插入后,Array 容器的基数是五个,对于由 16 位最高有效位表示的键。
4.2. Roaring Bitmap 的 Bitmap 容器
Bitmap 容器是位集的经典实现。
roaring bitmap 使用 long 数组来存储位图数据。与 Array 容器不同,数组容量固定为 1024。Bitmap 容器不需要找到位置。相反,它直接访问索引。
为了观察它的工作原理,我们将使用一个简单的示例。我们将数字 32786 插入到 roaring bitmap 中。前 16 位是 0000 0000 0000 0000。其余的位是 1000 0000 0001 0010 或十进制表示的 32786。这个值表示要在位图容器中设置的索引。让我们看看我们的 roaring bitmap 带有新信息:
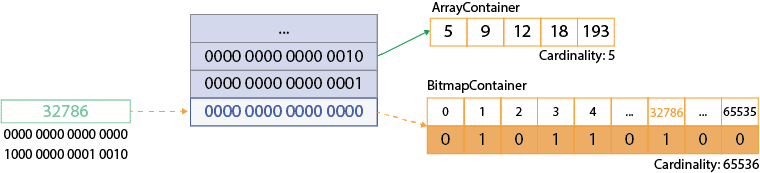
4.3. RoaringBitmap 的 Run 容器
当位图的某个区域有大量干净的单词时,Run-length 编码是最佳的容器选择。它使用 short 数据类型数组。
偶数索引处的值表示运行的开始,奇数索引处的值表示这些运行的长度。容器的基数是通过遍历完整的运行数组来计算的。
例如,以下图像向我们展示了一个具有连续整数序列的容器。然后,在 RLE 执行后,容器只剩下四个值:
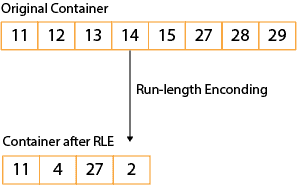
这些值表示为 11 后面跟着四个连续递增的值和 27 后面跟着两个连续递增的值。
这种压缩算法的工作方式取决于数据的紧凑性或连续性。如果我们有 100 个 short,它们都是一排的,它可以将它们从 200 字节压缩到四个字节,但如果它们都在不同的地方,编码后将从 200 字节变为 400 字节。
RoaringBitmap 中的并集
在对 roaring bitmap 进行了简要介绍之后,在我们进入代码示例之前,我们需要将 RoaringBitmap 依赖项添加到我们的 pom.xml 文件中:
``<dependency>```
```<groupId>```org.roaringbitmap```</groupId>```
```<artifactId>```RoaringBitmap```</artifactId>```
```<version>```0.9.38```</version>```
```</dependency>```
集合的并集是我们在 roaring bitmap 上测试的第一个操作。首先,让我们声明两个 RoaringBitmap 实例。第一个是 A,第二个是 B:
@Test
void givenTwoRoaringBitmap_whenUsingOr_thenWillGetSetsUnion() {
RoaringBitmap expected = RoaringBitmap.bitmapOf(1, 2, 3, 4, 5, 6, 7, 8);
RoaringBitmap A = RoaringBitmap.bitmapOf(1, 2, 3, 4, 5);
RoaringBitmap B = RoaringBitmap.bitmapOf(4, 5, 6, 7, 8);
RoaringBitmap union = RoaringBitmap.or(A, B);
assertEquals(expected, union);
}
在上述代码中,我们声明了我们的两个 RoaringBitmap 实例。我们使用 RoaringBitmap 提供的 bitmapOf() 静态工厂方法进行实例创建。然后,我们使用 or() 方法执行集合并集操作。在幕后,这个操作在集合位图之间完成了逻辑 OR。这是一个线程安全的操作。
RoaringBitmap 中的交集
我们可以在集合上执行的另一个有用操作是交集。
让我们为交集问题实现我们的测试用例。像并集一样,交集操作在 RoaringBitmap 中非常简单:
@Test
void givenTwoRoaringBitmap_whenUsingAnd_thenWillGetSetsIntersection() {
RoaringBitmap expected = RoaringBitmap.bitmapOf(4, 5);
RoaringBitmap A = RoaringBitmap.bitmapOfRange(1, 6);
RoaringBitmap B = RoaringBitmap.bitmapOf(4, 5, 6, 7, 8);
RoaringBitmap intersection = RoaringBitmap.and(A, B);
assertEquals(expected, intersection);
}
在这个测试用例中,我们使用 RoaringBitmap 类的另一个静态工厂方法声明 A 集合。bitmapOfRange() 静态方法创建一个新的 RoaringBitmap。在幕后,bitmapOfRange() 方法创建了一个新的实例,并使用 add() 方法将一系列数据添加到 roaring bitmap 中。在这种情况下,add() 方法接收两个 long 值作为参数,表示下限和上限。下限是包含的。与此相比,上限不包含在结果集的范围中。接收两个 int 值参数的 add() 方法在当前 API 版本中已弃用。
然后,我们使用 and() 方法执行我们的交集操作。正如其名称所建议的,and() 方法在两个集合之间执行逻辑 AND 操作。这个操作是线程安全的。
RoaringBitmap 中的差集
除了并集和交集,我们还有集合的相对补集操作。
接下来,让我们构建我们的 RoaringBitmap 集合差集的测试用例:
@Test
void givenTwoRoaringBitmap_whenUsingAndNot_thenWillGetSetsDifference() {
RoaringBitmap expected = RoaringBitmap.bitmapOf(1, 2, 3);
RoaringBitmap A = new RoaringBitmap();
A.add(1L, 6L);
RoaringBitmap B = RoaringBitmap.bitmapOf(4, 5, 6, 7, 8);
RoaringBitmap difference = RoaringBitmap.andNot(A, B);
assertEquals(expected, difference);
}
像我们之前的代码示例一样,我们声明了 A 和 B 两个集合。我们使用不同的方法来实例化这个案例中的 A 集合。我们首先创建一个空的 RoaringBitmap。然后,我们使用 add() 方法,与前面部分描述的 bitmapOfRange() 方法使用的方法相同。
andNot() 方法执行 A 和 B 之间的集合差集。从逻辑角度来看,这个操作执行了一个位的 ANDNOT(差集)操作。只要给定的位图保持不变,这个操作就是线程安全的。
RoaringBitmap 中的 XOR 操作
除了并集、交集和差集,我们还有 roaring bitmap 中的 XOR(异或)操作。这个操作类似于集合的相对补集,但是两个集合之间的公共元素会从结果集中省略。
我们使用 xor() 方法来执行这个操作。让我们看看我们的测试代码示例:
@Test
void givenTwoRoaringBitmap_whenUsingXOR_thenWillGetSetsSymmetricDifference() {
RoaringBitmap expected = RoaringBitmap.bitmapOf(1, 2, 3, 6, 7, 8);
RoaringBitmap A = RoaringBitmap.bitmapOfRange(1, 6);
RoaringBitmap B = RoaringBitmap.bitmapOfRange(4, 9);
RoaringBitmap xor = RoaringBitmap.xor(A, B);
assertEquals(expected, xor);
}
简而言之,RoaringBitmap 类中的 xor() 方法执行位的 XOR 操作,并且是线程安全的。
与 BitSet 的性能比较
此外,让我们在 RoaringBitmap 和 Java BitSet 之间构建一个简单的性能测试。对于每种集合类,我们测试了前面描述的操作:并集、交集、差集和 XOR。
我们使用 Java Microbenchmark Harness (JMH) 来实现我们的性能测试。首先,我们需要将依赖项添加到我们的 pom.xml 文件中:
``<dependency>``
```<groupId>```org.openjdk.jmh```</groupId>```
```<artifactId>```jmh-generator-annprocess```</artifactId>```
```<version>```1.37```</version>```
```</dependency>```
``<dependency>``
```<groupId>```org.openjdk.jmh```</groupId>```
```<artifactId>```jmh-core```</artifactId>```
```<version>```1.37```</version>```
```</dependency>```
JMH Core 和 JMH Annotation Processor 依赖项的最新版本可以在 Maven Central 中找到
9.1. 声明基准测试范围
接下来,我们声明我们的类和集合,就像我们为测试设置初始条件一样:
@State(Scope.Thread)
class BitSetsBenchmark {
private RoaringBitmap rb1;
private BitSet bs1;
private RoaringBitmap rb2;
private BitSet bs2;
private final static int SIZE = 10_000_000;
}
最初,我们声明了两种类型的两个集合,BitSet 和 RoaringBitmap。然后,我们设置了一个最大大小。SIZE 变量是我们将用作集合大小的上界。
我们将在这个类中执行所有的测试。此外,我们使用 State 的 Scope.Thread 和默认的 Throughput 基准测试模式。
我们将在操作后生成一个新的集合,以避免改变我们的输入数据结构。避免变异对于并发上下文很重要。这就是为什么,对于 BitSet 案例,我们将克隆输入集合,以便结果数据不会改变输入集合。
9.2. 基准测试数据设置
接下来,让我们为测试设置数据:
@Setup
public void setup() {
rb1 = new RoaringBitmap();
bs1 = new BitSet(SIZE);
rb2 = new RoaringBitmap();
bs2 = new BitSet(SIZE);
for (int i = 0; i < SIZE / 2; i++) {
rb1.add(i);
bs1.set(i);
}
for (int i = SIZE / 2; i < SIZE; i++) {
rb2.add(i);
bs2.set(i);
}
}
我们的两个 BitSet 集合被初始化为 SIZE。然后,对于第一个 RoaringBitmap 和 BitSet,我们添加/设置值直到 SIZE / 2,不包括在内。对于另外两个集合,我们从 SIZE / 2 添加值到 SIZE。
9.3. 基准测试
最后,让我们编写我们的测试。让我们从并集操作开始:
@Benchmark
public RoaringBitmap roaringBitmapUnion() {
return RoaringBitmap.or(rb1, rb2);
}
@Benchmark
public BitSet bitSetUnion() {
BitSet result = (BitSet) bs1.clone();
result.or(bs2);
return result;
}
第二个操作是交集:
@Benchmark
public RoaringBitmap roaringBitmapIntersection() {
return RoaringBitmap.and(rb1, rb2);
}
@Benchmark
public BitSet bitSetIntersection() {
BitSet result = (BitSet) bs1.clone();
result.and(bs2);
return result;
}
第三个是差集:
@Benchmark
public RoaringBitmap roaringBitmapDifference() {
return RoaringBitmap.andNot(rb1, rb2);
}
@Benchmark
public BitSet bitSetDifference() {
BitSet result = (BitSet) bs1.clone();
result.andNot(bs2);
return result;
}
最后一个是 XOR 操作:
@Benchmark
public RoaringBitmap roaringBitmapXOR() {
return RoaringBitmap.xor(rb1, rb2);
}
@Benchmark
public BitSet bitSetXOR() {
BitSet result = (BitSet) bs1.clone();
result.xor(bs2);
return result;
}
9.4. 基准测试结果
在执行我们的基准测试后,我们得到了以下结果:
Benchmark Mode Cnt Score Error Units
BitSetsBenchmark.bitSetDifference thrpt 25 3890.694 ± 313.808 ops/s
BitSetsBenchmark.bitSetIntersection thrpt 25 3542.387 ± 296.007 ops/s
BitSetsBenchmark.bitSetUnion thrpt 25 3012.666 ± 503.821 ops/s
BitSetsBenchmark.bitSetXOR thrpt 25 2872.402 ± 348.099 ops/s
BitSetsBenchmark.roaringBitmapDifference thrpt 25 12930.064 ± 527.289 ops/s
BitSetsBenchmark.roaringBitmapIntersection thrpt 25 824167.502 ± 30176.431 ops/s
BitSetsBenchmark.roaringBitmapUnion thrpt 25 6287.477 ± 250.657 ops/s
BitSetsBenchmark.roaringBitmapXOR thrpt 25 6060.993 ± 607.562 ops/s
正如我们所注意到的,RoaringBitmap 的性能优于 BitSet 操作。尽管有这些结果,我们需要考虑何时使用每种类型。
在某些情况下,尝试使用压缩位图是浪费的。例如,这可能是当我们有一个小的数据宇宙时。如果我们可以在不增加内存使用的情况下解压缩 BitSet,那么压缩位图可能不适合我们。如果不需要压缩,BitSet 提供了卓越的速度。
结论
在本文中,我们学习了 roaring bitmap 数据结构。我们讨论了 RoaringBitmap 的一些操作。此外,我们进行了 RoaringBitmap 和 BitSet 之间的一些性能测试。结果表明,前者的性能优于后者。
像往常一样,包含我们示例的源代码可以在 GitHub 上找到。
OK