Prim算法在Kotlin中的实现
Prim算法在Kotlin中的实现
1. 引言
在本教程中,我们将深入了解Prim算法。我们将了解它是什么以及如何在Kotlin中实现它。
2. 什么是Prim算法?
Prim算法是一种贪心算法,用于为加权无向图找到最小生成树。 这是什么意思呢?
无向图是一种边没有方向的图。也就是说,我们可以沿着任何边的任一方向遍历。加权意味着每条边都有一个与之相关联的成本或权重:
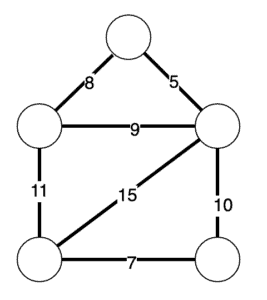
生成树是我们图中的边的一个子集,使得所有的节点都被连接起来。如果我们有一个加权图,我们的生成树的权重等同于所有使用边的总和。既然如此,最小生成树就是可能的生成树中权重最低的那一个:
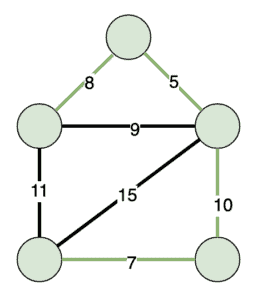
Prim算法允许我们在图中找到这样的最小生成树。
为了实现这一点,我们首先将图中的任意一个节点标记为已访问,并将所有其他节点标记为未访问:
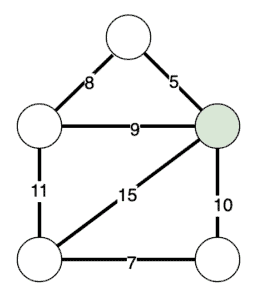
然后算法如下:
- 找到已访问节点和未访问节点之间的边,其权重最低。
- 将这条边添加到我们的生成树中。
- 将新节点标记为已访问。
- 假设还有我们没有访问过的节点,那么就重复这个过程。一旦我们访问了每个节点,我们就完成了。
这将迭代地找到我们的最小生成树:
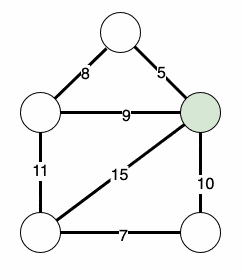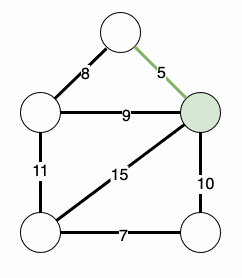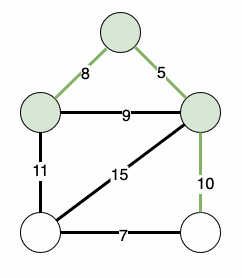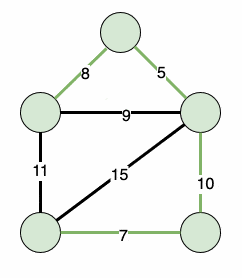
3. 实现Prim算法
现在我们已经看到了Prim算法,让我们看看如何在Kotlin中实现它。
3.1. 表示图
我们需要做的第一件事就是能够表示我们的图。这意味着一些边的集合,每条边由它连接的两个节点和该边的权重组成。
为了本文的目的,我们将节点表示为字符串。这些可以被视为节点的ID。实际上,我们可能想要使用更丰富的类型。唯一重要的是识别两个节点是相同的。
然后我们的_Edge_可以是一个数据类,包含这两个字符串和一个权重值:
data class Edge(
val first: String,
val second: String,
val weight: Int
)
现在,我们需要_Graph_本身。这只是一个边的集合,因为边可以给我们节点:
data class Graph(val edges: Collection```<Edge>```)
这意味着我们不能表示任何断开连接的节点——即没有边的节点——但它们无论如何都不能成为生成树的一部分。
我们还将向_Graph_类添加一些辅助方法。第一个是给我们图中所有节点的集合:
fun getNodes(): Collection``<String>`` {
return edges.flatMap { setOf(it.first, it.second) }.distinct()
}
第二个将为我们提供与给定节点相关联的所有边:
fun getEdgesForNode(node: String): Collection```<Edge>``` {
return edges.filter { it.first == node || it.second == node }
}
3.2. 准备算法
现在我们已经有了图的表示,我们可以实现我们的算法。 我们将这作为一个自由函数来实现,它以图作为输入,并返回一个只包含我们最小生成树边的图:
fun prims(graph: Graph): Graph {
// 算法在这里。
}
我们首先需要的是几个集合——一个用于我们已经访问过的节点集合,一个用于我们将要包含在我们的结果中的边集合:
val visitedNodes = mutableSetOf``<String>``()
val edges = mutableSetOf```<Edge>```()
我们还需要选择一个起始节点。这可以是图中的任何节点,所以我们将随机获取一个并将其添加到我们的已访问节点集合中:
visitedNodes.add(graph.getNodes().random())
我们同样可以使用返回的第一个节点、拥有最多边的节点或我们希望的任何其他方法。
3.3. 选择边
现在我们已经具备了起始条件,我们准备选择边。这是算法的核心。
在每次迭代中,我们需要选择一条从已访问节点到未访问节点的边,并且具有最小权重。让我们分解一下。
我们首先需要的是所有来自已访问节点的边。我们可以通过将我们的已访问节点集合映射到该节点的边,使用我们之前编写的辅助函数来做到这一点:
val allEdges = visitedNodes.flatMap { graph.getEdgesForNode(it) }
接下来,我们需要过滤这些边,只包括那些通向未访问节点的边。注意,我们不知道这条边的两个节点中的哪一个是哪一个,但我们也不关心。至少可以保证其中一个是已访问的节点——否则我们就不会考虑它——所以我们需要看看其中之一是否是未访问的节点:
val unvisitedEdges = allEdges.filter { !visitedNodes.contains(it.first) || !visitedNodes.contains(it.second) }
现在我们有了这组边,我们需要找到权重最低的那一条。这仅仅是按权重对集合进行排序,并取出列表中的第一个。然而,Kotlin为我们提供了_minBy_函数,它将为我们一步完成这项工作:
val nextEdge = unvisitedEdges.minBy { it.weight }
在这一点上,我们可以将节点标记为已访问,并将这条边添加到我们的结果中。同样,我们不知道这条边的_first_或_second_节点哪一个是我们的未访问节点,但这并不重要。因为我们在_Set_中存储我们的已访问节点,我们可以只添加它们两个,并相信_Set_会做正确的事情:
visitedNodes.addAll(setOf(nextEdge.first, nextEdge.second))
edges.add(nextEdge)
现在,我们只需要重复这个过程,直到我们访问了每个节点:
while (!visitedNodes.containsAll(graph.getNodes())) {
val nextEdge = visitedNodes.flatMap { graph.getEdgesForNode(it) }
.filter { !visitedNodes.contains(it.first) || !visitedNodes.contains(it.second) }
.minBy { it.weight }
visitedNodes.addAll(setOf(nextEdge.first, nextEdge.second))
edges.add(nextEdge)
}
4. 测试算法
现在我们已经得到了我们的算法,让我们确保它工作正常。 我们将从前面的例子图开始,只是我们现在给节点加上了标签:
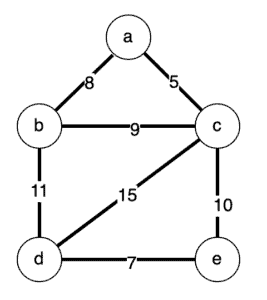
我们可以用我们的_Graph_类来表示这个:
val graph = Graph(setOf(
Edge(first = "a", second = "b", weight = 8),
Edge(first = "a", second = "c", weight = 5),
Edge(first = "b", second = "c", weight = 9),
Edge(first = "b", second = "d", weight = 11),
Edge(first = "c", second = "d", weight = 15),
Edge(first = "c", second = "e", weight = 10),
Edge(first = "d", second = "e", weight = 7)
))
如果我们在调用这个函数并输出结果,我们将看到:
Graph(edges=[
Edge(first=a, second=c, weight=5),
Edge(first=a, second=b, weight=8),
Edge(first=c, second=e, weight=10),
Edge(first=d, second=e, weight=7)
])
所以,我们的算法选择了我们之前看到的四条边。
5. 断开的图
如果我们尝试在断开的图上使用这个算法会发生什么? 也就是说,图中有些节点并不都是连接的:
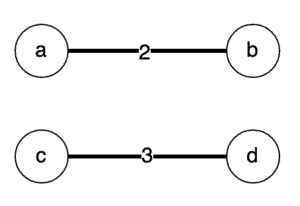
让我们尝试一下:
val graph = Graph(setOf(
Edge(first = "a", second = "b", weight = 2),
Edge(first = "c", second = "d", weight = 3),
))
prims(graph)
当我们运行这个时,我们不会得到一个新的_Graph_返回,其中包含我们的最小生成树,而是抛出了一个_NoSuchElementException_。 这是因为算法达到了一个