Java BigInteger 指南
Java BigInteger 指南
1. 引言
Java 提供了一些基本类型,如 int 或 long,用于执行整数运算。但有时,我们需要存储的数字会超出这些数据类型的可用限制。
在本教程中,我们将更深入地了解 BigInteger 类。我们将通过查看源代码来检查其结构,并回答这个问题——如何可能存储超出可用基本数据类型限制的大数字?
2. BigInteger 类
众所周知,BigInteger 类用于涉及比基本 long 类型更大的非常大的整数计算的数学运算。它表示不可变的任意精度整数。
在进一步讨论之前,让我们记住,在 Java 中所有字节都使用二进制补码系统并以大端序表示。它将一个字的最重要字节存储在最小的内存地址(最低索引)。此外,字节的最高位也是符号位。让我们检查一些示例字节值:
1000 0000表示-1280111 1111表示 1271111 1111表示-1
现在,让我们检查源代码并解释它如何存储超出基本数据类型限制的给定数字。
2.1. int signum
signum 属性确定 BigInteger 的符号。三个整数值表示值的符号:-1 表示负数,0 表示零,1 表示正数:
assertEquals(1, BigInteger.TEN.signum());
assertEquals(-1, BigInteger.TEN.negate().signum());
assertEquals(0, BigInteger.ZERO.signum());
让我们注意,BigInteger.ZERO 必须有 signum 的 0 由于大小数组。这个值确保每个 BigInteger 值恰好有一种表示。
2.2. int[] mag
BigInteger 类的所有魔力始于 mag 属性。它使用二进制表示将给定值存储在数组中,这允许省略基本数据类型限制。
此外,BigInteger 将它们分组为 32 位部分——一组四个字节。因此,类定义中的大小内部声明为 int 数组:
int[] mag;
这个数组以大端序表示持有给定值的大小。这个数组的零元素是大小的最重要 int。让我们使用 BigInteger(byte[] bytes) 来检查它:
assertEquals(new BigInteger("1"), new BigInteger(new byte[]{0b1}));
assertEquals(new BigInteger("2"), new BigInteger(new byte[]{0b10}));
assertEquals(new BigInteger("4"), new BigInteger(new byte[]{0b100}));
这个构造函数将包含二进制补码二进制表示的给定字节数组转换为值。
由于有符号-大小变量(signum),我们不使用第一个位作为值的符号位。让我们快速检查它:
byte[] bytes = { -128 }; // 1000 0000
assertEquals(new BigInteger("128"), new BigInteger(1, bytes));
assertEquals(new BigInteger("-128"), new BigInteger(-1, bytes));
我们使用 BigInteger(int signum, byte[] magnitude) 构造函数创建了两个不同的值。它将符号-大小表示转换为 BigInteger。我们重用了相同的字节数组,只改变了符号值。
我们还可以使用方法 toString(int radix) 打印大小:
assertEquals("10000000", new BigInteger(1, bytes));
assertEquals("-10000000", new BigInteger(-1, bytes));
注意,对于负值,添加了负号。
最后,大小的最显著 int 必须非零。这意味着 BigInteger.ZERO 有一个零长度的 mag 数组:
assertEquals(0, BigInteger.ZERO.bitCount());
assertEquals(BigInteger.ZERO, new BigInteger(0, new byte[]{}));
现在,我们将跳过检查其他属性。它们被标记为已弃用,因为冗余,仅用作内部缓存。
让我们现在直接进行更复杂的例子,并检查 BigInteger 如何存储超过基本数据类型的数字。
3. 大于 Long.MAX_VALUE 的 BigInteger
正如我们已经知道的,long 数据类型是一个 64 位二进制补码整数。有符号的长整数的最小值是 -263 (1000 0000 … 0000),最大值是 263-1 (0111 1111 … 1111)。要创建超出这些限制的数字,我们需要使用 BigInteger 类。
现在让我们创建一个比 Long.MAX_VALUE 大一个的值,等于 263。根据前一章的信息,它需要:
signum属性设置为 1,mag数组,总共 64 位,其中只有最高位设置(1000 0000 … 0000)。
首先,让我们使用 setBit(int n) 函数创建一个 BigInteger:
BigInteger bi1 = BigInteger.ZERO.setBit(63);
String str = bi1.toString(2);
assertEquals(64, bi1.bitLength());
assertEquals(1, bi1.signum());
assertEquals("9223372036854775808", bi1.toString());
assertEquals(BigInteger.ONE, bi1.substract(BigInteger.valueOf(Long.MAX_VALUE)));
assertEquals(64, str.length());
assertTrue(str.matches("^10{63}$")); // 1000 0000 ... 0000
记住,在二进制表示系统中,位从右到左按顺序排列,从 0 开始。虽然 BigInteger.ZERO 有一个空的大小数组,但设置第 63 位使其同时成为最重要的——64 长度数组的零元素。_signum_ 自动设置为一。
另一方面,相同的位序列由 Long.MIN_VALUE 表示。让我们将这个常量转换为 byte[] 数组并构造 BigInteger:
byte[] bytes = ByteBuffer.allocate(Long.BYTES).putLong(Long.MIN_VALUE).array();
BigInteger bi2 = new BigInteger(1, bytes);
assertEquals(bi1, bi2);
...
正如我们所看到的,这两个值是相等的,因此相同的断言集适用。
最后,我们可以检查内部的 int[] mag 变量。目前,Java 不提供 API 来获取这个值,但我们可以通过调试器中的评估工具来做:
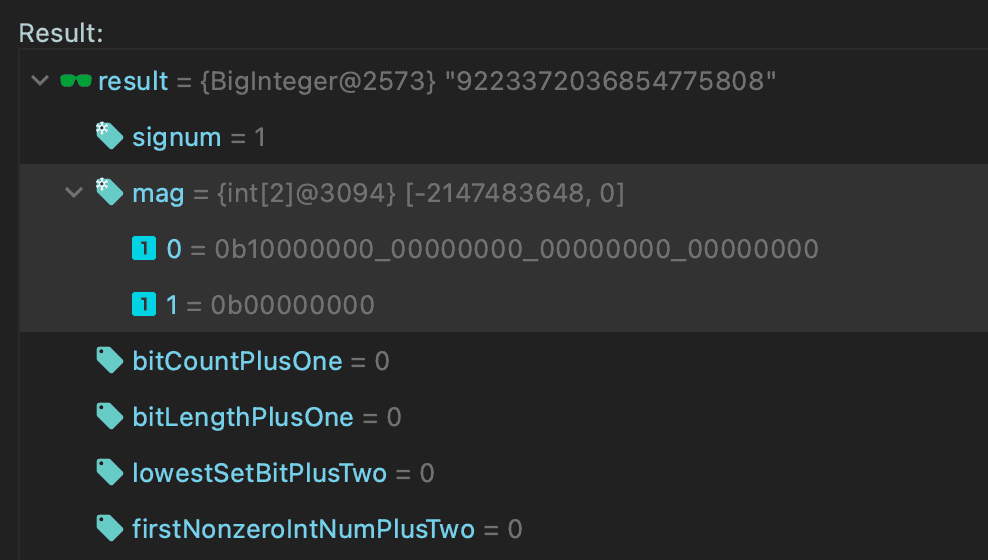
我们使用两个整数,两个 32 位的包将我们的值存储在数组中。零元素等于 Integer.MIN_VALUE,另一个是零。
4. 结论
在这个简短的教程中,我们专注于 BigInteger 类的实现细节。我们首先回顾了一些关于数字、基本类型和二进制表示规则的信息。
然后我们检查了 BigInteger 的源代码。我们检查了 signum 和 mag 属性。我们还学习了 BigInteger 如何存储给定的值,允许我们提供比基本数据类型更大的数字。
像往常一样,我们可以在 GitHub 上找到所有的代码片段和测试。