如何在Java中实现最小-最大堆
如何在Java中实现最小-最大堆
在本教程中,我们将探讨如何在Java中实现最小-最大堆。
首先,让我们看看堆的定义和特性。最小-最大堆是一个完整的二叉树,同时具有最小堆和最大堆的特性:
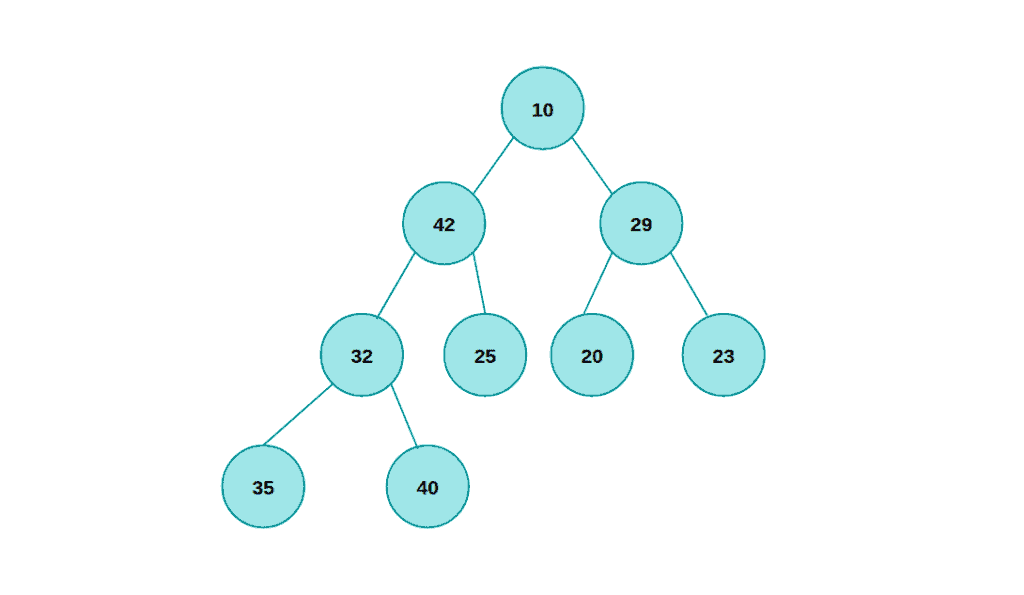
如上图所示,树中每个偶数层的节点都小于其所有后代,而每个奇数层的节点都大于其所有后代,根节点位于第零层。
最小-最大堆中的每个节点都有一个数据成员,通常称为键。根节点在最小-最大堆中具有最小的键,第二层的两个节点之一是最大的键。对于最小-最大堆中的每个节点X:
- 如果X在最小(或偶数)层,则X.key是在以X为根的子树中所有键中的最小键
- 如果X在最大(或奇数)层,则X.key是在以X为根的子树中所有键中的最大键
像最小堆或最大堆一样,插入和删除可以在O(logN)的时间复杂度内完成。
3.1. 创建
首先,让我们看看如何从现有数组构建最小-最大堆。这里我们使用Floyd算法,并进行了一些适应性修改,类似于堆化算法:
public List`````<T>````` create() {
for (int i = Math.floorDiv(array.size(), 2); i >= 1; i--) {
pushDown(array, i);
}
return array;
}
让我们通过查看上面的代码中的pushDown来更详细地了解发生了什么:
private void pushDown(List`````<T>````` array, int i) {
if (isEvenLevel(i)) {
pushDownMin(array, i);
} else {
pushDownMax(array, i);
}
}
如上所示,对于所有偶数层,我们使用pushDownMin检查数组项。这个算法就像我们将用于removeMin和removeMax的堆化下算法:
private void pushDownMin(List`````<T>````` h, int i) {
while (getLeftChildIndex(i) `< indicator) {
int indexOfSmallest = getIndexOfSmallestChildOrGrandChild(h, i);
//...
i = indexOfSmallest;
}
}
首先,我们找到'i'元素的最小子节点或孙子节点的索引。然后我们根据以下条件进行操作。
如果最小子节点或孙子节点不小于当前元素,我们就会中断。换句话说,元素的当前排列就像最小堆一样:
if (h.get(indexOfSmallest - 1).compareTo(h.get(i - 1)) < 0) {
//...
} else {
break;
}
如果最小子节点或孙子节点小于当前元素,我们将其与其父节点或祖父节点交换:
if (getParentIndex(getParentIndex(indexOfSmallest)) == i) {
if (h.get(indexOfSmallest - 1).compareTo(h.get(i - 1)) < 0) {
swap(indexOfSmallest - 1, i - 1, h);
if (h.get(indexOfSmallest - 1)
.compareTo(h.get(getParentIndex(indexOfSmallest) - 1)) >` 0) {
swap(indexOfSmallest - 1, getParentIndex(indexOfSmallest) - 1, h);
}
}
} else if (h.get(indexOfSmallest - 1).compareTo(h.get(i - 1)) < 0) {
swap(indexOfSmallest - 1, i - 1, h);
}
我们将继续上述操作,直到为元素'i'找到一个子节点。
现在,让我们看看getIndexOfSmallestChildOrGrandChild是如何工作的。这很简单!首先,我们假设左子节点具有最小值,然后与其他节点进行比较:
private int getIndexOfSmallestChildOrGrandChild(List`````<T>````` h, int i) {
int minIndex = getLeftChildIndex(i);
T minValue = h.get(minIndex - 1);
// 其余实现
}
在每一步中,如果索引大于指示器,则找到的最后一个最小值是答案。
例如,让我们将min-value与右子节点进行比较:
if (getRightChildIndex(i) `< indicator) {
if (h.get(getRightChildIndex(i) - 1).compareTo(minValue) < 0) {
minValue = h.get(getRightChildIndex(i));
minIndex = getRightChildIndex(i);
}
} else {
return minIndex;
}
现在,让我们创建一个测试来验证从无序数组创建最小-最大堆是否正常工作:
@Test
public void givenUnOrderedArray_WhenCreateMinMaxHeap_ThenIsEqualWithMinMaxHeapOrdered() {
List`<Integer>`` list = Arrays.asList(34, 12, 28, 9, 30, 19, 1, 40);
MinMaxHeap`<Integer>` minMaxHeap = new MinMaxHeap<>(list);
minMaxHeap.create();
Assert.assertEquals(List.of(1, 40, 34, 9, 30, 19, 28, 12), list);
}
_pushDownMax_算法与_pushDownMin_相同,只是所有比较运算符都相反。
3.2. 插入
让我们看看如何将一个元素添加到最小-最大堆中:
public void insert(T item) {
if (isEmpty()) {
array.add(item);
indicator++;
} else if (!isFull()) {
array.add(item);
pushUp(array, indicator);
indicator++;
} else {
throw new RuntimeException("invalid operation !!!");
}
}
首先,我们检查堆是否为空。如果堆为空,我们添加新元素并增加指示器。否则,添加的新元素可能会改变最小-最大堆的顺序,所以我们需要用pushUp调整堆:
private void pushUp(List`````<T>`````h,int i) {
if (i != 1) {
if (isEvenLevel(i)) {
if (h.get(i - 1).compareTo(h.get(getParentIndex(i) - 1)) `< 0) {
pushUpMin(h, i);
} else {
swap(i - 1, getParentIndex(i) - 1, h);
i = getParentIndex(i);
pushUpMax(h, i);
}
} else if (h.get(i - 1).compareTo(h.get(getParentIndex(i) - 1)) >` 0) {
pushUpMax(h, i);
} else {
swap(i - 1, getParentIndex(i) - 1, h);
i = getParentIndex(i);
pushUpMin(h, i);
}
}
}
如上所示,新元素与其父节点进行比较,然后:
- 如果发现它小于(大于)父节点,那么它肯定小于(大于)所有其他在最大(最小)层上的元素,这些元素在堆的根路径上
- 新元素到根的路径(只考虑最小/最大层)应该是按降序(升序)排列的,就像插入之前一样。因此,我们需要将新元素进行二元插入到这个序列中
现在,让我们看看pushUpMin是如何进行的:
private void pushUpMin(List`````<T>````` h , int i) {
while(hasGrandparent(i) && h.get(i - 1)
.compareTo(h.get(getGrandparentIndex(i) - 1)) < 0) {
swap(i - 1, getGrandparentIndex(i) - 1, h);
i = getGrandparentIndex(i);
}
}
技术上,当父节点更大时,交换新元素与其父节点更简单。同样,pushUpMax与pushUpMin相同,只是所有比较运算符都相反。
现在,让我们创建一个测试来验证将新元素插入到最小-最大堆中是否正常工作:
@Test
public void givenNewElement_WhenInserted_ThenIsEqualWithMinMaxHeapOrdered() {
MinMaxHeap`<Integer>` minMaxHeap = new MinMaxHeap<>(8);
minMaxHeap.insert(34);
minMaxHeap.insert(12);
minMaxHeap.insert(28);
minMaxHeap.insert(9);
minMaxHeap.insert(30);
minMaxHeap.insert(19);
minMaxHeap.insert(1);
minMaxHeap.insert(40);
Assert.assertEquals(List.of(1, 40, 28, 12, 30, 19, 9, 34),
minMaxHeap.getMinMaxHeap());
}
3.3. 查找最小值
最小-最大堆中的主要元素始终位于根节点,所以我们可以在O(1)的时间复杂度内找到它:
public T min() {
if (!isEmpty()) {
return array.get(0);
}
return null;
}
3.4. 查找最大值
最小-最大堆中的最大元素始终位于第一个奇数层,所以我们可以在O(1)的时间复杂度内通过简单比较找到它:
public T max() {
if (!isEmpty()) {
if (indicator == 2) {
return array.get(0);
}
if (indicator == 3) {
return array.get(1);
}
return array.get(1).compareTo(array.get(2)) < 0 ? array.get(2) : array.get(1);
}
return null;
}
3.5. 移除最小值
在这种情况下,我们将找到最小元素,然后用数组的最后一个元素替换它:
public T removeMin() {
T min = min();
if (min != null) {
if (indicator == 2) {
array.remove(indicator--);
return min;
}
array.set(0, array.get(--indicator - 1));
array.remove(indicator - 1);
pushDown(array, 1);
}
return min;
}
3.6. 移除最大值
移除最大元素与移除最小元素相同,唯一的变化是我们找到最大元素的索引,然后调用pushDown:
public T removeMax() {
T max = max();
if (max != null) {
int maxIndex;
if (indicator == 2) {
maxIndex = 0;
array.remove(--indicator - 1);
return max;
} else if (indicator == 3) {
maxIndex = 1;
array.remove(--indicator - 1);
return max;
} else {
maxIndex = array.get(1).compareTo(array.get(2)) < 0 ? 2 : 1;
}
array.set(maxIndex, array.get(--indicator - 1));
array.remove(indicator - 1);
pushDown(array, maxIndex + 1);
}
return max;
}
4. 结论
在本教程中,我们看到了如何在Java中实现最小-最大堆,并探索了一些最常见的操作。
首先,我们了解了什么是最小-最大堆,包括一些最常见的特性。然后,我们看到了如何在最小-最大堆中创建、插入、查找最小值、查找最大值、移除最小值和移除最大值。
像往常一样,本文中使用的所有示例都可以在GitHub上找到。