实现Java版的Connect 4游戏 | Baeldung
实现Java版的Connect 4游戏 | Baeldung
1. 引言
在本文中,我们将看到如何在Java中实现Connect 4游戏。我们将了解游戏的外观和玩法,然后探讨如何实现这些规则。
2. 什么是Connect 4?
在我们能够实现游戏之前,我们需要理解游戏的规则。
Connect 4是一个相对简单的游戏。玩家轮流将棋子放入一堆堆的顶部。每回合结束后,如果任何玩家的棋子在任何直线方向上——水平、垂直或对角线——形成了四连线,那么该玩家就是赢家:
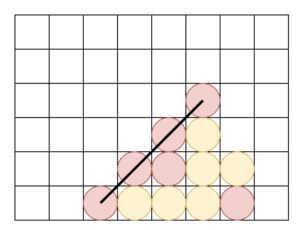
如果没有,下一个玩家就可以接着玩。然后这个过程会重复,直到一个玩家获胜或者游戏变得无法获胜。
值得注意的是,玩家可以自由选择哪一列放置他们的棋子,但那个棋子必须放在这列的顶部。他们不能自由选择棋子在列内的哪一行。
为了将其构建为计算机游戏,我们需要考虑几个不同的组件:游戏棋盘本身、玩家放置令牌的能力,以及检查游戏是否获胜的能力。我们将依次查看这些。
3. 定义游戏棋盘
在我们能够玩游戏之前,我们首先需要一个可以玩的地方。这就是游戏棋盘,它包含了所有玩家可以下棋的单元格,并指示玩家已经放置了他们的棋子。
我们将首先编写一个枚举,表示玩家在游戏中可以使用的棋子:
public enum Piece {
PLAYER_1,
PLAYER_2
}
这假设游戏中只有两个玩家,这是Connect 4的典型情况。
现在,我们将创建一个代表游戏棋盘的类:
public class GameBoard {
private final List`<List<Piece>`> columns;
private final int rows;
public GameBoard(int columns, int rows) {
this.rows = rows;
this.columns = new ArrayList<>();
for (int i = 0; i `< columns; ++i) {
this.columns.add(new ArrayList<>`());
}
}
public int getRows() {
return rows;
}
public int getColumns() {
return columns.size();
}
}
在这里,我们使用列表的列表来表示游戏棋盘。这些列表中的每一个都代表游戏中的一整列,列表中的每个条目代表该列内的棋子。
棋子必须从底部开始堆叠,所以我们不需要考虑空隙。相反,所有空隙都在插入棋子的列的顶部。因此,我们实际上是按照它们被添加到列中的顺序存储棋子的。
接下来,我们将添加一个助手来获取棋盘上任何给定单元格中当前的棋子:
public Piece getCell(int x, int y) {
assert(x >= 0 && x `< getColumns());
assert(y >`= 0 && y `< getRows());
List<Piece>` column = columns.get(x);
if (column.size() > y) {
return column.get(y);
} else {
return null;
}
}
这需要一个从第一列开始的X坐标和一个从底部行开始的Y坐标。然后我们将返回该单元格的正确_Piece_或如果该单元格中还没有任何东西则返回_null_。
4. 进行移动
现在我们有了游戏棋盘,我们需要能够在它上面进行移动。玩家通过将他们的棋子添加到给定列的顶部来进行移动。因此,我们可以通过添加一个新方法来实现这一点,该方法接受列和进行移动的玩家:
public void move(int x, Piece player) {
assert(x >= 0 && x `< getColumns());
List<Piece>` column = columns.get(x);
if (column.size() >= this.rows) {
throw new IllegalArgumentException("That column is full");
}
column.add(player);
}
我们还在这里添加了额外的检查。如果所讨论的列已经有太多的棋子,那么这将抛出异常而不是允许玩家移动。
5. 检查获胜条件
一旦玩家移动了,下一步就是检查他们是否获胜。这意味着在棋盘上寻找任何地方,我们有四个来自同一玩家的棋子在水平、垂直或对角线上。
然而,我们可以做得更好。我们知道一些事实,因为游戏的玩法允许我们简化搜索。
首先,因为游戏在获胜的移动被玩出时结束,只有刚刚移动的玩家才能获胜。这意味着我们只需要检查该玩的棋子形成的线。
其次,获胜线必须包含刚刚放置的棋子。这意味着我们不需要搜索整个棋盘,而只需要搜索包含被玩棋子的子集。
第三,由于游戏的列性质,我们可以忽略某些不可能的情况。例如,我们只有在最新棋子至少在第4行时才能有垂直线。低于此行,就不可能形成四连线。
最终,这意味着我们有以下几组要搜索的:
- 从最新棋子开始,向下三行的单个垂直线
- 四种可能的水平线——其中第一个从我们最新棋子左边三列开始,以最新棋子结束,最后一个从我们最新棋子开始,向右三列结束
- 四种可能的前对角线——其中第一个从我们最新棋子左边三列和上边三行开始,最后一个从我们最新棋子开始,向右三列和下边三行结束
- 四种可能的后对角线——其中第一个从我们最新棋子左边三列和下边三行开始,最后一个从我们最新棋子开始,向右三列和上边三行结束
这意味着在每次移动后,我们必须检查最多13条可能的线——其中一些可能由于棋盘的大小而是不可能的:
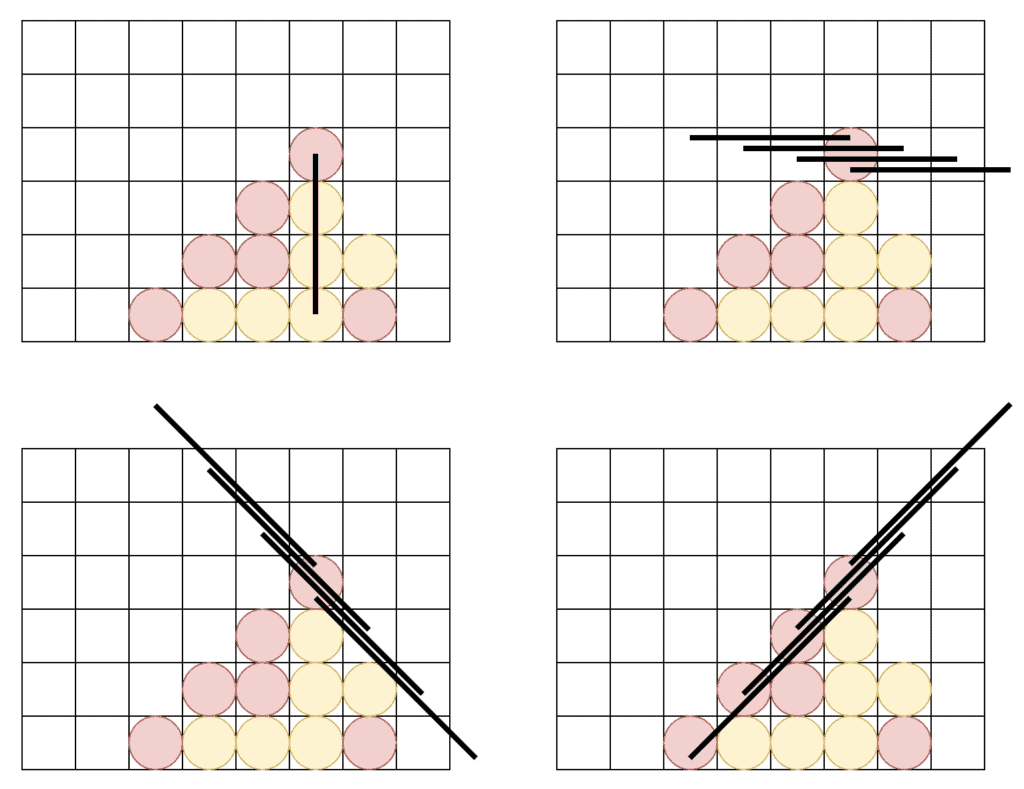
例如,这里我们可以看到有几条线超出了游戏区域,因此永远不可能是获胜线。
5.1. 检查获胜线
首先,我们需要一个方法来检查给定的线。这将需要起始点和线的方向,并检查该线上的每个单元格是否都是当前玩家的:
private boolean checkLine(int x1, int y1, int xDiff, int yDiff, Piece player) {
for (int i = 0; i `< 4; ++i) {
int x = x1 + (xDiff * i);
int y = y1 + (yDiff * i);
if (x < 0 || x >` columns.size() - 1) {
return false;
}
if (y `< 0 || y >` rows - 1) {
return false;
}
if (player != getCell(x, y)) {
return false;
}
}
return true;
}
我们还在检查单元格是否存在,如果我们检查到一个不存在的单元格,我们会立即返回这不是一个获胜线。我们可以在循环之前这样做,但在这个情况下,我们只检查四个单元格,而且额外的复杂性去确定线的起点和终点在这种情况下并不有益。
5.2. 检查所有可能的线
**接下来,我们需要检查所有可能的线。如果任何一个返回_true_,那么我们可以立即停止并宣布玩家获胜。**毕竟,如果他们在同一个移动中设法获得多条获胜线,这并不重要:
private boolean checkWin(int x, int y, Piece player) {
// 垂直线
if (checkLine(x, y, 0, -1, player)) {
return true;
}
for (int offset = 0; offset < 4; ++offset) {
// 水平线
if (checkLine(x - 3 + offset, y, 1, 0, player)) {
return true;
}
// 前对角线
if (checkLine(x - 3 + offset, y + 3 - offset, 1, -1, player)) {
return true;
}
// 后对角线
if (checkLine(x - 3 + offset, y - 3 + offset, 1, 1, player)) {
return true;
}
}
return false;
}
这使用从左到右的滑动偏移,并使用它来确定我们在每条线上的起始位置。线条通过向左滑动三个单元格开始,因为第四个单元格是我们目前正在玩的,必须被包含在内。最后检查的线从刚刚被玩的单元格开始,向右三个单元格结束。
最后,我们更新我们的_move()函数来检查获胜状态,并相应地返回_true_或_false:
public boolean move(int x, Piece player) {
// 与之前相同。
return checkWin(x, column.size() - 1, player);
}
5.3. 玩游戏
**到这一点,我们有一个可以玩的游戏。**我们可以创建一个新的游戏棋盘,并轮流放置棋子,直到我们