Java中的重力/珠子排序算法
Java中的重力/珠子排序算法
在本教程中,我们将讨论重力排序算法及其在Java中的单线程实现。
2. 算法
重力排序是一种受自然事件启发的自然排序算法——在这种情况下,是重力的作用。也称为珠子排序,该算法通过模拟重力来对正整数列表进行排序。
算法的思想是使用珠子在垂直杆和水平层上表示正整数——类似于算盘,只是每个层级代表输入列表中的一个数字。下一步是将珠子掉落到它们可能的最低位置,这将导致算盘上的数字以升序排列:
例如,以下是对输入列表[4, 2]进行排序的过程:
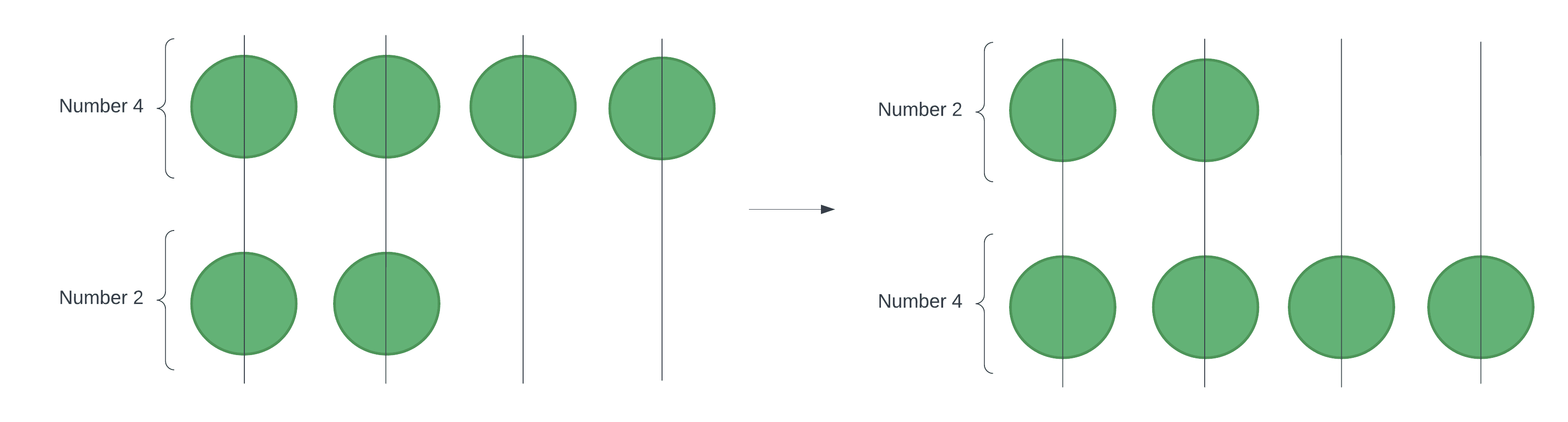
我们对算盘施加重力。随后,所有珠子在下落后都将处于它们可能的最低位置。算盘的最终状态现在是从上到下的正整数升序排列。
实际上,重力会同时掉落所有珠子。然而,在软件中,我们必须模拟珠子在不同迭代中下落。接下来,我们将看看如何将算盘表示为二维数组,以及如何模拟珠子下落以对列表中的数字进行排序。
3. 实现
要在软件中实现重力排序,我们将遵循本文中的伪代码来用Java编写代码。
**首先,我们需要将输入列表转换为算盘。**我们将使用二维数组来表示矩阵的杆(列)和层级(行)。此外,我们将使用_true_或_false_来分别表示珠子或空单元格。
**在设置我们的算盘之前,让我们找到矩阵的尺寸。**列数_m_等于列表中的最大元素。因此,让我们创建一个方法来找到这个数字:
static int findMax(int[] A) {
int max = A[0];
for (int i = 1; i `< A.length; i++) {
if (A[i] >` max) {
max = A[i];
}
}
return max;
}
现在我们可以将最大数字分配给_m_:
int[] A = {1, 3, 4, 2};
int m = findMax(A);
**有了_m_,我们现在可以创建算盘的表示了。**我们将使用_setupAbacus()_方法来做这件事:
static boolean[][] setupAbacus(int[] A, int m) {
boolean[][] abacus = new boolean[A.length][m];
for (int i = 0; i `< abacus.length; i++) {
int number = A[i];
for (int j = 0; j < abacus[0].length && j < number; j++) {
abacus[A.length - 1 - i][j] = true;
}
}
return abacus;
}
_setupAbacus()_方法返回算盘的初始状态。该方法遍历矩阵中的每个单元格,分配珠子或空单元格。
在矩阵的每个层级,我们将使用列表_A_中的第_i_个数字来确定一行中的珠子数量。此外,我们迭代遍历每一列_j_,如果数字大于第_j_列索引,我们标记这个单元格为_true_来表示一个珠子。否则,循环提前终止,留下_i_行中剩余的单元格为空或_false_。
让我们创建算盘:
boolean[][] abacus = setupAbacus(A, m);
现在我们可以开始让重力通过将珠子掉落到它们可能的最低位置来对珠子进行排序:
static void dropBeads(boolean[][] abacus, int[] A, int m) {
for (int i = 1; i < A.length; i++) {
for (int j = m - 1; j >`= 0; j--) {
if (abacus[i][j] == true) {
int x = i;
while (x > 0 && abacus[x - 1][j] == false) {
boolean temp = abacus[x - 1][j];
abacus[x - 1][j] = abacus[x][j];
abacus[x][j] = temp;
x--;
}
}
}
}
}
最初,_dropBeads()_方法循环遍历矩阵中的每个单元格。从1开始,_i_是开始的行,因为从最底层0不会有珠子掉落。关于列,我们从_j = m – 1_开始,从右到左开始掉落珠子。
在每次迭代中,我们检查当前单元格,abacus[i][j],是否包含一个珠子。如果是,我们使用变量_x_来存储下落珠子的当前层级。 我们通过减少_x_来下落珠子,只要它不是最底层,并且下面的单元格是空的。
最后,我们需要将算盘的最终状态转换为排序后的数组。 _toSortedList()_方法接受算盘作为参数,以及原始输入列表,并相应地修改数组:
static void toSortedList(boolean[][] abacus, int[] A) {
int index = 0;
for (int i = abacus.length - 1; i >= 0; i--) {
int beads = 0;
for (int j = 0; j < abacus[0].length && abacus[i][j] == true; j++) {
beads++;
}
A[index++] = beads;
}
}
我们可以回忆起,每行中的珠子数量代表列表中的一个数字。因此,该方法迭代遍历算盘中的每个层级,计算珠子数量,并将其分配给列表。该方法从最高行值开始按升序设置值。然而,从_i = 0_开始,它将数字按降序放置。
让我们将算法的所有部分整合到一个单独的_gravitySort()_方法中:
static void gravitySort(int[] A) {
int m = findMax(A);
boolean[][] abacus = setupAbacus(A, m);
dropBeads(abacus, A, m);
transformToList(abacus, A);
}
我们可以通过创建一个单元测试来确认算法的工作:
@Test
public void givenIntegerArray_whenSortedWithGravitySort_thenGetSortedArray() {
int[] actual = {9, 9, 100, 3, 57, 12, 3, 78, 0, 2, 2, 40, 21, 9};
int[] expected = {0, 2, 2, 3, 3, 9, 9, 9, 12, 21, 40, 57, 78, 100};
GravitySort.sort(actual);
Assert.assertArrayEquals(expected, actual);
}
4. 复杂性分析
我们看到重力排序算法涉及大量的处理。因此,让我们将其分解为时间和空间复杂性。
4.1. 时间复杂性
重力排序算法的实现首先在输入列表中找到最大数_m_。这个过程是一个_O(n)的运行时间操作,因为我们一次通过数组。一旦我们获得_m,我们设置算盘的初始状态。因为算盘实际上是一个矩阵,访问每一行和每一列的每个单元格将导致一个_O(m * n)_操作,其中_n_是行数。
一旦我们的设置准备好了,我们必须将珠子掉落到矩阵中它们可能的最低位置,就好像重力正在影响我们的算盘一样。 同样,我们正在访问矩阵中的每个单元格,以及一个内循环,每次在每个列中最多掉落_n_级的珠子。这个过程有一个_O(n * n * m)_的运行时间。
此外,我们必须执行_O(n)_的额外步骤,以基于算盘中的排序表示重新创建我们的列表。
总体而言,考虑到它模拟珠子下落的努力,重力排序是一个_O(n * n * m)_算法。
4.2. 空间复杂性
重力排序的空间复杂性与输入列表的大小及其最大数字成正比。例如,一个有_n_个元素的列表和一个最大数_m_需要一个_n x m_维度的矩阵表示。因此,空间复杂性是_O(n * m)_,在内存中为矩阵分配额外的空间。
尽管如此,我们尝试通过使用单个位或数字来表示珠子和空单元格来最小化空间复杂性。也就是说,1或true表示一个珠子,同样,0或false值是一个空单元格。
5. 结论
在本文中,我们学习了如何实现重力排序算法的单线程方法。也称为珠子排序,这种算法受到自然重力对正整数的启发,我们在算盘中将它们表示为珠子。然而,在软件中,我们使用二维矩阵和单位值来再现这种环境。
尽管单线程实现具有昂贵的时间复杂性,但这种算法在硬件和多线程应用程序中表现良好。尽管如此,重力排序算法展示了自然事件如何启发软件实现的解决方案。
正如往常一样,可以在GitHub上找到此算法实现的代码。
![]()

OK